Negative Zahlen bezwingen: Addieren und Subtrahieren im Griff
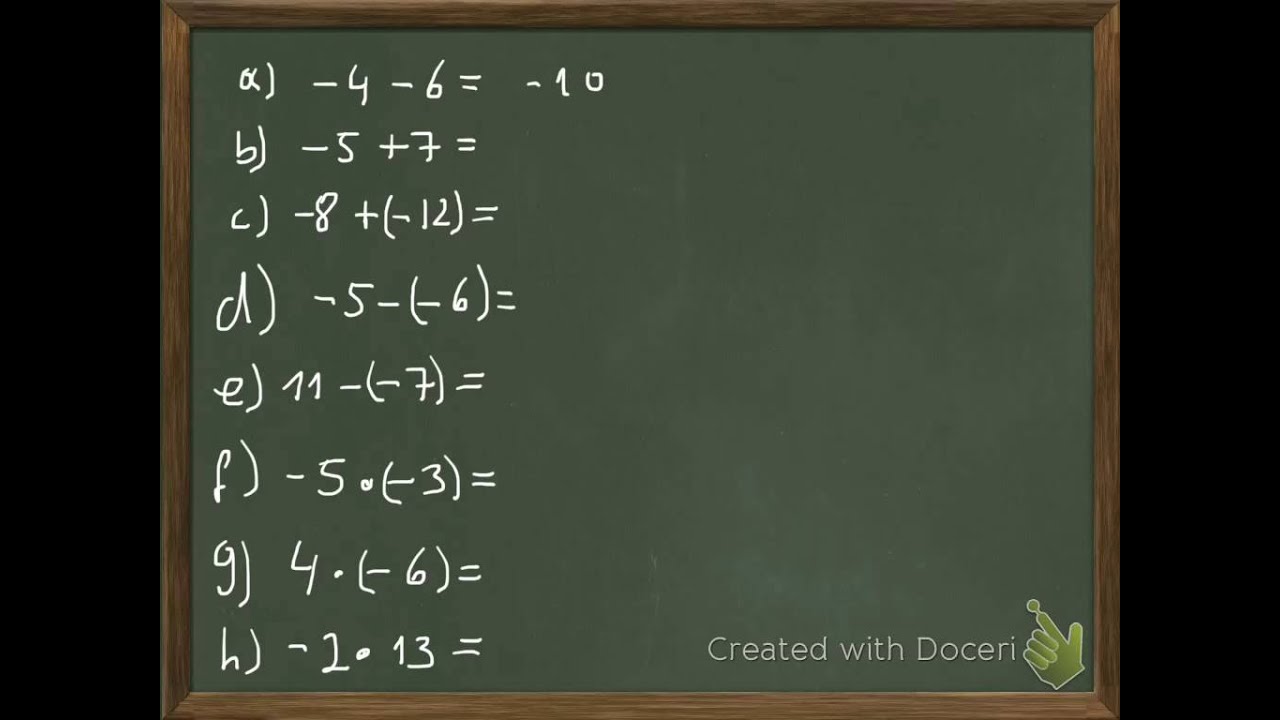
Stehst du vor dem Rätsel negativer Zahlen? Fühlst du dich unsicher, wenn es darum geht, sie zu addieren oder zu subtrahieren? Keine Sorge, du bist nicht allein! Viele Menschen finden den Umgang mit negativen Zahlen zunächst verwirrend. Dieser Artikel führt dich Schritt für Schritt durch die Welt des Rechnens mit negativen Zahlen, von den Grundlagen bis hin zu fortgeschrittenen Konzepten.
Negative Zahlen begegnen uns im Alltag häufiger, als man vielleicht denkt: Temperaturen unter dem Gefrierpunkt, Schulden auf dem Konto oder Höhenangaben unter dem Meeresspiegel. Das Verständnis des Rechnens mit negativen Zahlen ist daher unerlässlich, um diese alltäglichen Situationen zu meistern und mathematische Probleme zu lösen.
Die Geschichte der negativen Zahlen reicht weit zurück. Während positive Zahlen zum Zählen konkreter Objekte verwendet wurden, hatten negative Zahlen lange Zeit einen abstrakteren Charakter. Sie wurden zunächst als "Schulden" oder "fehlende Größen" interpretiert. Erst im Laufe der Zeit wurden sie als eigenständige Zahlen anerkannt und in das Zahlensystem integriert.
Das Rechnen mit negativen Zahlen ermöglicht es uns, mathematische Modelle für eine Vielzahl von Phänomenen zu erstellen, von der Physik bis zur Finanzwelt. Es ist ein grundlegendes Werkzeug in der Algebra und bildet die Basis für komplexere mathematische Operationen.
Ein Hauptproblem beim Umgang mit negativen Zahlen liegt in der Vorstellung und Interpretation. Die Idee einer "negativen Größe" kann zunächst schwer fassbar sein. Die Regeln der Addition und Subtraktion negativer Zahlen unterscheiden sich von denen positiver Zahlen und erfordern daher ein Umdenken.
Die Addition negativer Zahlen lässt sich am besten mit dem Zahlenstrahl veranschaulichen. Addiert man eine negative Zahl, bewegt man sich auf dem Zahlenstrahl nach links. Beispiel: -3 + (-5) = -8. Man startet bei -3 und bewegt sich 5 Einheiten nach links, was zu -8 führt. Subtrahiert man eine negative Zahl, ist dies gleichbedeutend mit der Addition der entsprechenden positiven Zahl. Beispiel: -3 - (-5) = -3 + 5 = 2.
Die Subtraktion negativer Zahlen kann ebenfalls am Zahlenstrahl visualisiert werden. Subtrahiert man eine negative Zahl, bewegt man sich nach rechts. -3 - (-5) entspricht einer Bewegung von 5 Einheiten nach rechts von -3, was zu 2 führt.
Vorteile des Rechnens mit negativen Zahlen: 1. Beschreibung von realen Phänomenen wie Temperaturen unter Null. 2. Erweiterung des mathematischen Werkzeugkastens für komplexere Berechnungen. 3. Entwicklung des abstrakten Denkens.
Aktionsplan: 1. Verstehe die Grundlagen der Addition und Subtraktion positiver Zahlen. 2. Visualisiere negative Zahlen am Zahlenstrahl. 3. Übe mit verschiedenen Beispielen. 4. Integriere negative Zahlen in reale Problemstellungen.
Vor- und Nachteile des Rechnens mit negativen Zahlen
| Vorteile | Nachteile |
|---|---|
| Beschreibung realer Phänomene | Abstraktes Konzept, anfänglich schwer verständlich |
| Erweiterung mathematischer Möglichkeiten | Verwechslungsgefahr mit den Rechenregeln für positive Zahlen |
FAQ:
1. Was ist eine negative Zahl? Eine Zahl kleiner als Null.
2. Wie addiert man negative Zahlen? Addiert man zwei negative Zahlen, so addiert man die Beträge und setzt ein Minuszeichen davor.
3. Wie subtrahiert man negative Zahlen? Subtrahiert man eine negative Zahl, so addiert man die entsprechende positive Zahl.
4. Wozu braucht man negative Zahlen? Zur Beschreibung von Größen unterhalb eines Referenzpunktes.
5. Was ist der Unterschied zwischen -5 und 5? -5 liegt links von Null auf dem Zahlenstrahl, 5 rechts davon.
6. Wie berechnet man -5 + 3? -2
7. Wie berechnet man -5 - (-3)? -2
8. Wie berechnet man 5 - (-3)? 8
Tipps und Tricks: Nutze den Zahlenstrahl zur Visualisierung. Denke an "Schulden" und "Guthaben". Übe regelmäßig.
Zusammenfassend lässt sich sagen, dass das Rechnen mit negativen Zahlen ein essentieller Bestandteil der Mathematik ist. Es ermöglicht uns, reale Phänomene zu beschreiben, komplexe Berechnungen durchzuführen und unser abstraktes Denken zu schulen. Obwohl das Konzept der negativen Zahlen zunächst herausfordernd sein kann, ist es mit Übung und den richtigen Werkzeugen wie dem Zahlenstrahl leicht zu meistern. Beginne noch heute damit, dich mit negativen Zahlen vertraut zu machen und entdecke die vielfältigen Möglichkeiten, die sie dir bieten!
Stadtgericht russellville alabama informationen
Gfy bedeutung im chat entdecke die volle form und ihre nutzung
Offentliche aufzeichnungen marion county florida ein einblick
