Découverte des Polygones jusqu'à 12 Côtés
Imaginez des formes, des figures géométriques, des constructions fascinantes. Entrez dans l'univers des polygones, ces figures fermées composées de segments de droites, et plus particulièrement, ceux qui possèdent jusqu'à douze côtés. Du triangle familier au dodécagone plus complexe, un monde de possibilités s'ouvre à nous.
Cet article vous propose une exploration complète des polygones ayant jusqu'à douze côtés. Nous aborderons leurs caractéristiques, leur histoire, et comment ils s'intègrent dans notre quotidien, souvent sans que nous nous en rendions compte. Préparez-vous à un voyage géométrique passionnant !
Les polygones sont partout autour de nous. Des panneaux de signalisation aux motifs architecturaux, en passant par les formes naturelles des cristaux, leur présence est omniprésente. Comprendre leurs propriétés, c'est décrypter une partie du langage de l'univers.
Des figures à trois côtés, les triangles, aux figures à douze côtés, les dodécagones, chaque polygone possède ses propres spécificités. Le nombre de côtés, la longueur de ces côtés, les angles, tout contribue à définir l'identité unique de chaque figure. Leur étude permet d'appréhender la complexité et la beauté de la géométrie.
Depuis l'Antiquité, les mathématiciens grecs, comme Euclide, ont étudié les polygones avec une grande rigueur. Leurs travaux ont posé les fondations de la géométrie telle que nous la connaissons aujourd'hui. L'étude des polygones ayant jusqu'à douze côtés, en particulier, a permis de comprendre des concepts fondamentaux comme les angles, les surfaces et les symétries.
Les polygones réguliers, ceux dont tous les côtés et tous les angles sont égaux, sont particulièrement intéressants. Le pentagone régulier, par exemple, se retrouve dans la nature, dans la forme de certaines fleurs. L'hexagone régulier, quant à lui, est la forme des alvéoles des abeilles, une structure d'une efficacité remarquable.
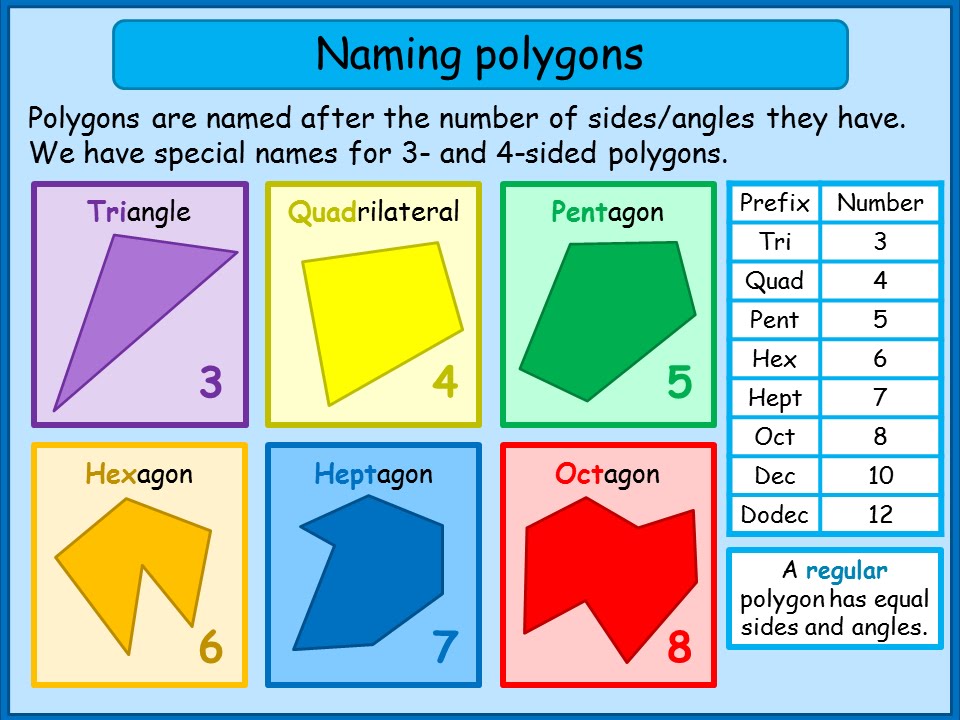
Un triangle est un polygone à 3 côtés. Un carré a 4 côtés. Un pentagone a 5 côtés. Un hexagone a 6 côtés. Un heptagone a 7 côtés. Un octogone a 8 côtés. Un nonagone a 9 côtés. Un décagone a 10 côtés. Un hendécagone a 11 côtés. Un dodécagone a 12 côtés. Ces figures peuvent être régulières ou irrégulières.
Un avantage des polygones est leur utilisation en architecture et en design. Leur variété de formes permet de créer des structures complexes et esthétiques. Un autre avantage réside dans leur utilisation en mathématiques pour comprendre des concepts géométriques plus avancés. Enfin, leur présence dans la nature nous aide à comprendre l'organisation du monde qui nous entoure.
Pour dessiner un polygone régulier, on peut utiliser un compas et une règle. Par exemple, pour un hexagone, on trace un cercle, puis on reporte six fois le rayon du cercle sur la circonférence. On relie ensuite les points obtenus pour former l'hexagone.
Conseils: N'oubliez pas que la somme des angles intérieurs d'un polygone à n côtés est égale à (n-2) x 180 degrés.
FAQ:
1. Qu'est-ce qu'un polygone? Réponse: Une figure géométrique plane fermée, composée de segments de droites.
2. Qu'est-ce qu'un polygone régulier? Réponse: Un polygone dont tous les côtés et tous les angles sont égaux.
3. Combien de côtés a un dodécagone? Réponse: 12 côtés.
4. Comment calculer l'aire d'un polygone? Réponse: Cela dépend du type de polygone. Il existe des formules spécifiques pour chaque type.
5. Où trouve-t-on des polygones dans la nature? Réponse: Dans les cristaux, les alvéoles des abeilles, les pétales de fleurs, etc.
6. Quelle est la différence entre un polygone convexe et un polygone concave? Réponse: Un polygone convexe n'a pas d'angle rentrant, tandis qu'un polygone concave en a au moins un.
7. Comment construire un polygone régulier? Réponse: On peut utiliser un compas et une règle.
8. Quelle est l'importance des polygones en mathématiques? Réponse: Ils sont fondamentaux pour la géométrie et permettent de comprendre des concepts plus complexes.
En conclusion, les polygones ayant jusqu'à douze côtés, du triangle au dodécagone, représentent un élément essentiel de la géométrie. Leur étude nous permet de comprendre les formes qui nous entourent, de l'architecture à la nature. De l'antiquité à nos jours, les mathématiciens ont exploré leurs propriétés, posant les bases de nombreuses découvertes. L'exploration de ces figures géométriques est une invitation à la découverte d'un monde fascinant, où la beauté et la rigueur mathématique se rejoignent. Continuez à explorer, à dessiner, à construire, et laissez-vous surprendre par la richesse des polygones. N'hésitez pas à approfondir vos connaissances sur ce sujet passionnant.
Signification du prenom maeve en irlandais
Dechainer la puissance de goku all star 6 etoiles guide ultime
Liberez votre kamehameha imprimez vos heros dragon ball z
