Décryptage de la Gravitation Universelle : Sa Formule et Ses Secrets
L'univers est un ballet incessant de corps célestes, une danse cosmique orchestrée par une force invisible mais omniprésente : la gravité. Mais comment quantifier cette interaction fondamentale ? La réponse réside dans la constante de gravitation universelle, une valeur numérique enchâssée au cœur de la physique. Ce concept, apparemment abstrait, est la clé pour comprendre les mouvements des planètes, la formation des étoiles et l'expansion de l'univers lui-même. Plongeons au cœur de cette notion essentielle et découvrons les secrets de l'équation qui régit l'attraction entre les masses.
La constante de gravitation universelle, souvent dénotée par la lettre G, est un paramètre fondamental de la loi de la gravitation universelle de Newton. Cette loi stipule que chaque particule de matière dans l'univers attire toute autre particule avec une force proportionnelle au produit de leurs masses et inversement proportionnelle au carré de la distance qui les sépare. G est le facteur de proportionnalité qui relie la force d'attraction à ces autres grandeurs. Sa valeur, déterminée expérimentalement, est extrêmement petite, reflétant la faiblesse relative de la force gravitationnelle à l'échelle humaine.
L'histoire de la constante gravitationnelle est intimement liée à celle de la physique classique. Si Newton a formulé la loi de la gravitation, il n'a pas déterminé la valeur exacte de G. Ce fut Henry Cavendish, un siècle plus tard, qui réalisa la première mesure précise de cette constante à l'aide d'une balance de torsion. Cette expérience, une véritable prouesse technique pour l'époque, permit de quantifier l'attraction entre des masses connues et d'en déduire la valeur de G. Cette découverte fut une étape cruciale pour la compréhension quantitative de la gravitation.
L'importance de la constante gravitationnelle est capitale. Elle est essentielle pour calculer la force d'attraction entre deux corps célestes, prédire les trajectoires des satellites, estimer la masse des planètes et même étudier l'expansion de l'univers. Sans la connaissance de G, l'astronomie moderne serait impossible. Cette constante est la pierre angulaire de notre compréhension de l'univers à grande échelle.
Malgré son importance fondamentale, la constante de gravitation universelle est aussi source de défis. Sa valeur est la moins précisément connue de toutes les constantes fondamentales de la physique. Les mesures expérimentales de G sont difficiles à réaliser et sujettes à des incertitudes. Cette imprécision limite notre capacité à modéliser certains phénomènes gravitationnels avec une grande exactitude. La recherche continue pour affiner la mesure de G et comprendre les raisons de ces difficultés.
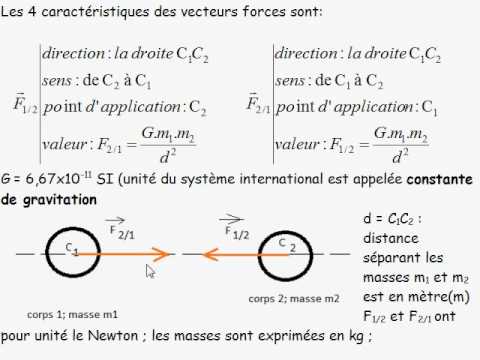
La formule de la loi de gravitation universelle de Newton est F = G * (m1 * m2) / r², où F est la force d'attraction, m1 et m2 sont les masses des deux objets, r est la distance entre leurs centres de masse et G est la constante de gravitation universelle. Cette équation permet de calculer la force gravitationnelle entre deux objets quelconques connaissant leurs masses et la distance qui les sépare.
Un exemple simple : Calculer la force d'attraction entre la Terre et la Lune. Connaissant les masses respectives et la distance qui les sépare, en appliquant la formule avec la valeur de G, on obtient la force gravitationnelle responsable du mouvement orbital de la Lune autour de la Terre.
Les avantages de connaître et d'utiliser la constante gravitationnelle sont nombreux. Elle permet de comprendre les interactions gravitationnelles, de prédire les mouvements des corps célestes et de calculer la masse des objets astronomiques. De plus, elle est essentielle pour les missions spatiales, le positionnement par satellite et la recherche en astrophysique.
FAQ:
1. Qu'est-ce que la constante de gravitation universelle ? Réponse : C’est une constante fondamentale qui dicte la force de l’attraction gravitationnelle entre deux objets.
2. Quelle est la formule de la loi de gravitation universelle ? Réponse : F = G * (m1 * m2) / r²
3. Qui a découvert la constante de gravitation universelle ? Réponse : Henry Cavendish a réalisé la première mesure précise.
4. Pourquoi la constante gravitationnelle est-elle importante ? Réponse : Elle est essentielle pour comprendre et calculer les interactions gravitationnelles.
5. Quelle est la valeur approximative de G ? Réponse : 6,674 x 10⁻¹¹ N⋅m²/kg²
6. Quelles sont les difficultés liées à la mesure de G ? Réponse : La faiblesse de la force gravitationnelle rend les mesures précises difficiles.
7. Comment la constante gravitationnelle est-elle utilisée en astronomie ? Réponse : Pour calculer les masses des planètes, les orbites des satellites, etc.
8. La constante gravitationnelle est-elle vraiment constante ? Réponse : C’est une question de recherche actuelle, mais on suppose généralement qu’elle est constante.
En conclusion, la constante de gravitation universelle, bien que discrète dans sa valeur numérique, joue un rôle colossal dans notre compréhension de l'univers. De la chute d'une pomme à la danse des galaxies, cette constante relie tous les objets massifs par une force invisible mais fondamentale. La recherche continue pour affiner sa mesure et explorer ses mystères, ouvrant la voie à des découvertes toujours plus profondes sur la nature de la gravité et l'évolution du cosmos. Continuer à explorer les implications de cette constante est essentiel pour déchiffrer les secrets de l'univers et repousser les frontières de notre connaissance.
Lunivers scintillant des casinos en ligne jouer pour de largent reel
Maitrisez lart de remplir les mots fleches
Decryptage du mystere de la lettre mantis dans starfield
